Portfolio Strategy: Portfolio Management¶
Introduction¶
Portfolio Strategy is designed to adopt different portfolio strategies, which means that users can adopt different algorithms to generate investment portfolios based on the prediction scores of the Forecast Model. Users can use the Portfolio Strategy in an automatic workflow by Workflow module, please refer to Workflow: Workflow Management.
Because the components in Qlib are designed in a loosely-coupled way, Portfolio Strategy can be used as an independent module also.
Qlib provides several implemented portfolio strategies. Also, Qlib supports custom strategy, users can customize strategies according to their own requirements.
After users specifying the models(forecasting signals) and strategies, running backtest will help users to check the performance of a custom model(forecasting signals)/strategy.
Base Class & Interface¶
BaseStrategy¶
Qlib provides a base class qlib.strategy.base.BaseStrategy. All strategy classes need to inherit the base class and implement its interface.
- generate_trade_decision
- generate_trade_decision is a key interface that generates trade decisions in each trading bar. The frequency to call this method depends on the executor frequency(“time_per_step”=”day” by default). But the trading frequency can be decided by users’ implementation. For example, if the user wants to trading in weekly while the time_per_step is “day” in executor, user can return non-empty TradeDecision weekly(otherwise return empty like this ).
Users can inherit BaseStrategy to customize their strategy class.
WeightStrategyBase¶
Qlib also provides a class qlib.contrib.strategy.WeightStrategyBase that is a subclass of BaseStrategy.
WeightStrategyBase only focuses on the target positions, and automatically generates an order list based on positions. It provides the generate_target_weight_position interface.
- generate_target_weight_position
- According to the current position and trading date to generate the target position. The cash is not considered in the output weight distribution.
- Return the target position.
Note
Here the target position means the target percentage of total assets.
WeightStrategyBase implements the interface generate_order_list, whose processions is as follows.
- Call generate_target_weight_position method to generate the target position.
- Generate the target amount of stocks from the target position.
- Generate the order list from the target amount
Users can inherit WeightStrategyBase and implement the interface generate_target_weight_position to customize their strategy class, which only focuses on the target positions.
Implemented Strategy¶
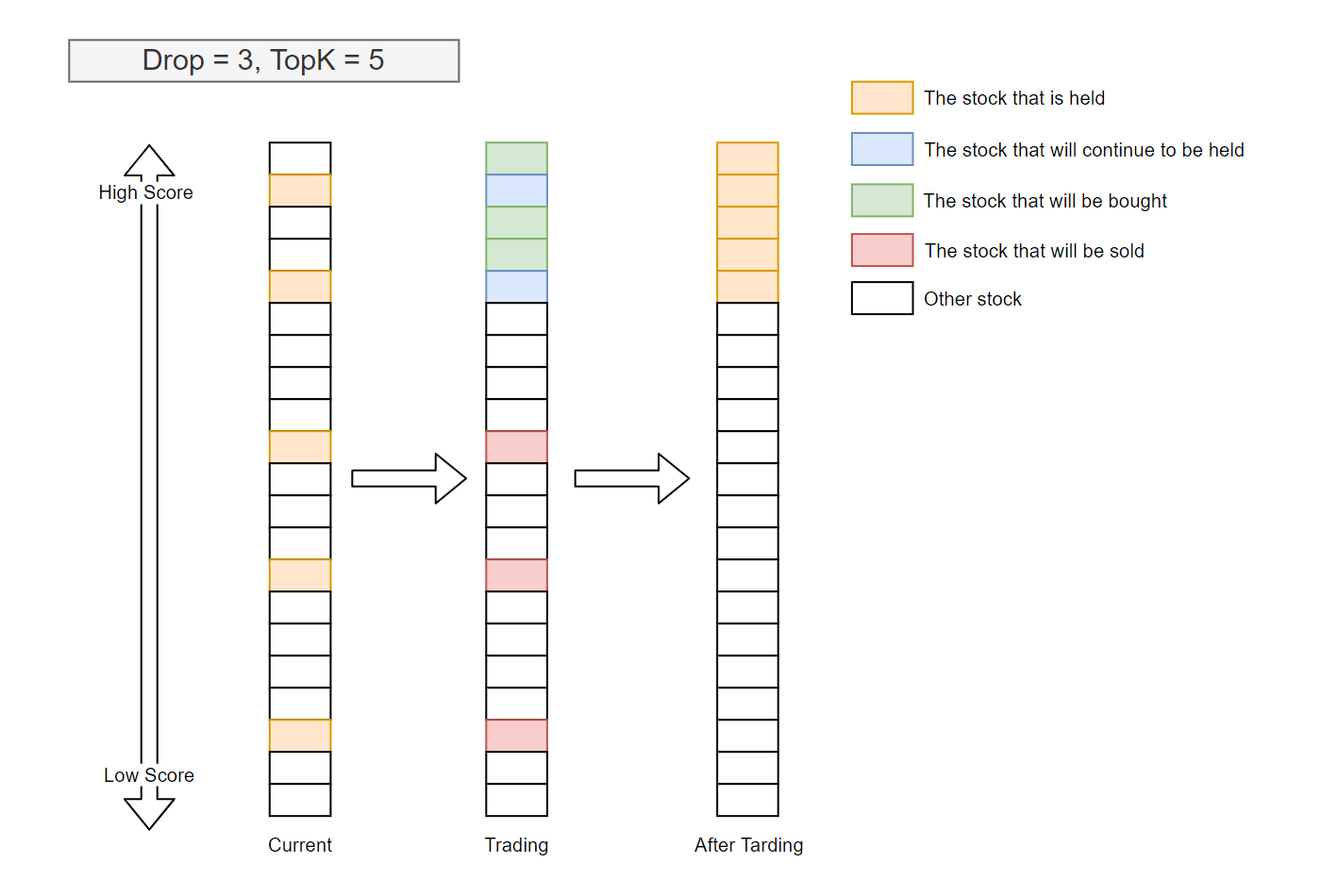
Qlib provides a implemented strategy classes named TopkDropoutStrategy.
TopkDropoutStrategy¶
TopkDropoutStrategy is a subclass of BaseStrategy and implement the interface generate_order_list whose process is as follows.
Adopt the
Topk-Dropalgorithm to calculate the target amount of each stockNote
There are two parameters for the
Topk-Dropalgorithm:- Topk: The number of stocks held
- Drop: The number of stocks sold on each trading day
In general, the number of stocks currently held is Topk, with the exception of being zero at the beginning period of trading. For each trading day, let $d$ be the number of the instruments currently held and with a rank $gt K$ when ranked by the prediction scores from high to low. Then d number of stocks currently held with the worst prediction score will be sold, and the same number of unheld stocks with the best prediction score will be bought.
In general, $d=$`Drop`, especially when the pool of the candidate instruments is large, $K$ is large, and Drop is small.
In most cases,
TopkDropalgorithm sells and buys Drop stocks every trading day, which yields a turnover rate of 2$times$`Drop`/$K$.The following images illustrate a typical scenario.
Generate the order list from the target amount
EnhancedIndexingStrategy¶
EnhancedIndexingStrategy Enhanced indexing combines the arts of active management and passive management, with the aim of outperforming a benchmark index (e.g., S&P 500) in terms of portfolio return while controlling the risk exposure (a.k.a. tracking error).
For more information, please refer to qlib.contrib.strategy.signal_strategy.EnhancedIndexingStrategy and qlib.contrib.strategy.optimizer.enhanced_indexing.EnhancedIndexingOptimizer.
Usage & Example¶
First, user can create a model to get trading signals(the variable name is pred_score in following cases).
Prediction Score¶
The prediction score is a pandas DataFrame. Its index is <datetime(pd.Timestamp), instrument(str)> and it must contains a score column.
A prediction sample is shown as follows.
datetime instrument score
2019-01-04 SH600000 -0.505488
2019-01-04 SZ002531 -0.320391
2019-01-04 SZ000999 0.583808
2019-01-04 SZ300569 0.819628
2019-01-04 SZ001696 -0.137140
... ...
2019-04-30 SZ000996 -1.027618
2019-04-30 SH603127 0.225677
2019-04-30 SH603126 0.462443
2019-04-30 SH603133 -0.302460
2019-04-30 SZ300760 -0.126383
Forecast Model module can make predictions, please refer to Forecast Model: Model Training & Prediction.
Normally, the prediction score is the output of the models. But some models are learned from a label with a different scale. So the scale of the prediction score may be different from your expectation(e.g. the return of instruments).
Qlib didn’t add a step to scale the prediction score to a unified scale due to the following reasons. - Because not every trading strategy cares about the scale(e.g. TopkDropoutStrategy only cares about the order). So the strategy is responsible for rescaling the prediction score(e.g. some portfolio-optimization-based strategies may require a meaningful scale). - The model has the flexibility to define the target, loss, and data processing. So we don’t think there is a silver bullet to rescale it back directly barely based on the model’s outputs. If you want to scale it back to some meaningful values(e.g. stock returns.), an intuitive solution is to create a regression model for the model’s recent outputs and your recent target values.
Running backtest¶
In most cases, users could backtest their portfolio management strategy with
backtest_daily.from pprint import pprint import qlib import pandas as pd from qlib.utils.time import Freq from qlib.utils import flatten_dict from qlib.contrib.evaluate import backtest_daily from qlib.contrib.evaluate import risk_analysis from qlib.contrib.strategy import TopkDropoutStrategy # init qlib qlib.init(provider_uri=<qlib data dir>) CSI300_BENCH = "SH000300" STRATEGY_CONFIG = { "topk": 50, "n_drop": 5, # pred_score, pd.Series "signal": pred_score, } strategy_obj = TopkDropoutStrategy(**STRATEGY_CONFIG) report_normal, positions_normal = backtest_daily( start_time="2017-01-01", end_time="2020-08-01", strategy=strategy_obj ) analysis = dict() # default frequency will be daily (i.e. "day") analysis["excess_return_without_cost"] = risk_analysis(report_normal["return"] - report_normal["bench"]) analysis["excess_return_with_cost"] = risk_analysis(report_normal["return"] - report_normal["bench"] - report_normal["cost"]) analysis_df = pd.concat(analysis) # type: pd.DataFrame pprint(analysis_df)
If users would like to control their strategies in a more detailed(e.g. users have a more advanced version of executor), user could follow this example.
from pprint import pprint import qlib import pandas as pd from qlib.utils.time import Freq from qlib.utils import flatten_dict from qlib.backtest import backtest, executor from qlib.contrib.evaluate import risk_analysis from qlib.contrib.strategy import TopkDropoutStrategy # init qlib qlib.init(provider_uri=<qlib data dir>) CSI300_BENCH = "SH000300" # Benchmark is for calculating the excess return of your strategy. # Its data format will be like **ONE normal instrument**. # For example, you can query its data with the code below # `D.features(["SH000300"], ["$close"], start_time='2010-01-01', end_time='2017-12-31', freq='day')` # It is different from the argument `market`, which indicates a universe of stocks (e.g. **A SET** of stocks like csi300) # For example, you can query all data from a stock market with the code below. # ` D.features(D.instruments(market='csi300'), ["$close"], start_time='2010-01-01', end_time='2017-12-31', freq='day')` FREQ = "day" STRATEGY_CONFIG = { "topk": 50, "n_drop": 5, # pred_score, pd.Series "signal": pred_score, } EXECUTOR_CONFIG = { "time_per_step": "day", "generate_portfolio_metrics": True, } backtest_config = { "start_time": "2017-01-01", "end_time": "2020-08-01", "account": 100000000, "benchmark": CSI300_BENCH, "exchange_kwargs": { "freq": FREQ, "limit_threshold": 0.095, "deal_price": "close", "open_cost": 0.0005, "close_cost": 0.0015, "min_cost": 5, }, } # strategy object strategy_obj = TopkDropoutStrategy(**STRATEGY_CONFIG) # executor object executor_obj = executor.SimulatorExecutor(**EXECUTOR_CONFIG) # backtest portfolio_metric_dict, indicator_dict = backtest(executor=executor_obj, strategy=strategy_obj, **backtest_config) analysis_freq = "{0}{1}".format(*Freq.parse(FREQ)) # backtest info report_normal, positions_normal = portfolio_metric_dict.get(analysis_freq) # analysis analysis = dict() analysis["excess_return_without_cost"] = risk_analysis( report_normal["return"] - report_normal["bench"], freq=analysis_freq ) analysis["excess_return_with_cost"] = risk_analysis( report_normal["return"] - report_normal["bench"] - report_normal["cost"], freq=analysis_freq ) analysis_df = pd.concat(analysis) # type: pd.DataFrame # log metrics analysis_dict = flatten_dict(analysis_df["risk"].unstack().T.to_dict()) # print out results pprint(f"The following are analysis results of benchmark return({analysis_freq}).") pprint(risk_analysis(report_normal["bench"], freq=analysis_freq)) pprint(f"The following are analysis results of the excess return without cost({analysis_freq}).") pprint(analysis["excess_return_without_cost"]) pprint(f"The following are analysis results of the excess return with cost({analysis_freq}).") pprint(analysis["excess_return_with_cost"])
Result¶
The backtest results are in the following form:
risk
excess_return_without_cost mean 0.000605
std 0.005481
annualized_return 0.152373
information_ratio 1.751319
max_drawdown -0.059055
excess_return_with_cost mean 0.000410
std 0.005478
annualized_return 0.103265
information_ratio 1.187411
max_drawdown -0.075024
- excess_return_without_cost
- mean
- Mean value of the CAR (cumulative abnormal return) without cost
- std
- The Standard Deviation of CAR (cumulative abnormal return) without cost.
- annualized_return
- The Annualized Rate of CAR (cumulative abnormal return) without cost.
- information_ratio
- The Information Ratio without cost. please refer to Information Ratio – IR.
- max_drawdown
- The Maximum Drawdown of CAR (cumulative abnormal return) without cost, please refer to Maximum Drawdown (MDD).
- excess_return_with_cost
- mean
- Mean value of the CAR (cumulative abnormal return) series with cost
- std
- The Standard Deviation of CAR (cumulative abnormal return) series with cost.
- annualized_return
- The Annualized Rate of CAR (cumulative abnormal return) with cost.
- information_ratio
- The Information Ratio with cost. please refer to Information Ratio – IR.
- max_drawdown
- The Maximum Drawdown of CAR (cumulative abnormal return) with cost, please refer to Maximum Drawdown (MDD).
Reference¶
To know more about the prediction score pred_score output by Forecast Model, please refer to Forecast Model: Model Training & Prediction.